Monthly Archives: July 2016

architecture, art, books, education, history, memoria, notes, paintings, sculptures, weekly book

Geometry of Design (II)

Elam, Kimberly. Geometry of Design: Studies in Proportion and Composition. New York: Princeton Architectural, 2001. Print.

See Fibonacci number

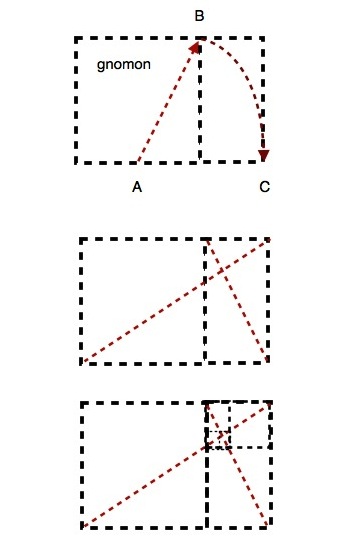
Golden section square construction Method p. 24

square-construction

AB         AC
—-   =   —–
AC          CB

A C B
|——————-|———|

“The golden section rectangle is unique in that when subdivided its reciprocal is a smaller proportional rectangle.” p. 25

Golden Section Spiral construction. p. 25

620/377 = 1.61803 Golden Section. p. 29

Golden Section Triangle and Ellipse p. 30

Golden Section Proportion of the Star Pentagram p. 31

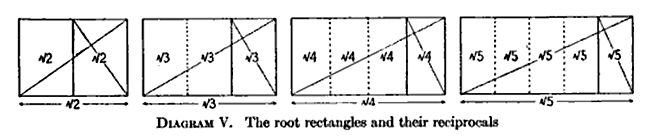
Root 2 Rectangle Construction (√2)  p. 34

Hambidge Fig. 10 showing construction of “root rectangles. 1920. from Dynamic symmetry: the Greek vase. Via Wikimedia.

Root 2 Rectangle Construction. Circle Method p. 35

DIN System of Paper Proportioning A1-A5

“Root 2 rectangles possess the special property of being endlessly subdivided by proportionally smaller rectangles. It is for this reason that the root 2 rectangle is the basis for the European DIN (Deutsche Industrie Normen), a system of paper sizes.” p. 36

Root 3 rectangle p. 38

Root 4 Rectangle p. 40.

Lacey Davis Caskey – Geometry of Greek Vases: Attic Vases in the Museum of Fine Arts Analysed According to the Principals of Proportion Discovered by Jay Hambidge. Via Wikimedia

See The Modulor by Le Corbusier

Le Corbusier: “the composition of of works of art is governed by by rules; these rules may be conscious methods, pointed and subtle, or they may be commonplace rules, tritely applied. They may also be implied by the creative instinct of the artist, a manifestation of an intuitive harmony,”  p. 43

See Jules Cheret and Star Pentagram proportions.

Hippodrome, Leona Dare, 1883. Via wikimedia.

See Belle Époque

See Bauhaus typeface.

See Oskar Schlemmer

1932 Schlemmer Treppenszene anagoria. Via Wikimedia.

See East Coast poster by Tom Purvis

Designed by Tom Purvis and believed to feature his son with a Meccano. Via Wikimedia.

Circles aligned in Wagon -Bar Poster by A.M. Cassandre, 1932.

А.М. Кассандр (1901 — 1968) Via Wikimedia.

See Constructivism

‘Proun Vrashchenia’ by El Lissitzky, 1919. Wikimedia.

See Die Neue Typographie (1928) by Jan Tschichold

Root 2 rectangles and circles in proportion p. 73

Type construction p. 74

See Max Bill

See Inge Druckrey

See Bruno Monguzzi

Le Corbusier (from Modulor, 1949):

“The regulating lines do not bring in any poetic or lyrical ideas; they do not inspire the theme of the work; they are not creative; they merely establish a balance.” p. 101.

“Biology, geometry, and art are taught as separate subjects. The content area of each that is congruent to the other is often neglected and the student is left to make the connections on their own. In addition, art and design are commonly viewed as intuitive endeavors and expressions of personal inspirations.” p. 101

Save

architecture, art, books, drawing, history, paintings, photography, sculptures, weekly book

Geometry of Design (I)

Elam, Kimberly. Geometry of Design: Studies in Proportion and Composition. New York: Princeton Architectural, 2001. Print.

“German psychologist, Gustav Fechner…. investigated the human response to the special aesthetic qualities of the golden section rectangle… Fechner limited his experiment to the man-made world and began by taking the measurements of thousand of rectangular objects such as books, boxes, buildings, matchbooks, newspapers, etc. He found that the average ratio was close to a ration known as the golden ration, 1:1.618, and that the majority of people prefer a rectangle whose proportions are close to the golden section.” p. 6-7.

Most preferred rectangle 5:8 according to Fechner (1876) and Lalo (1908).

Read The Curves of Life by Cook, Theodore Andrea, Sir, (1867-1928)

“there is an attempt in biological growth pattern proportion to approach but never reach golden spiral proportions.” p. 9

“the ration of any two lines within a star pentagram is the golden section proportion of 1:1.618.” p. 9

“The numbers 8 and 13 as found in the pine cone spiral and 21 and 34 as found in the sunflower spiral and 21 and 34 as found in the sunflower spiral… adjacent pairs in the mathematical sequence called the Fibonacci sequence.” p. 10.

“Vitruvius advised that the architecture of temples should be based on the likeness of the perfectly proportioned human body where a harmony exists among all parts.” p. 12

See Vitruvius (born c. 80–70 BC, died after c. 15 BC)

A 1684 depiction of Vitruvius (right) presenting De Architectura to Augustus. Sebastian Le Clerc. Via wikimedia.

See statue  Doryphoros (Δορυφόρος)

See statue Artemision Bronze

See Leornardo Da Vinci’s Human Figure in a Circle and Albrecht Dürer‘s Man Inscribed in a Circle

See facial proportions p. 18-19

“The Parthenon in Athens is an example of the Greek system of proportioning. In a simple analysis the façade of the parthenon is embraced by a subdivided golden rectangles.” p. 20

On the Cathedral of Notre Dame “The rectangle around the cathedral façade is in golden section proportion.” p. 21

“The clerestory window is in proportion of 1:4 to the major circle of the façade.” p. 21

“Even the earliest and most primitive architect developed the use of a regulating unit of measure such as a hand, or foot or forearm in order to systemize and bring order to the task.” p. 22-23.

Golden rectangle

Fibonacci number

Gnomon (figure)

 

 

Gold, silver, and bronze rectangles arranged vertically so that they are all the same width. Squares marked with dotted lines and arrows. Via Wikimedia.

Save

Save